MÁQUINAS DE ESTADOS (FINITE STATE MACHINE – FSM)
Una máquina de estados finitos (FSM) es una abstracción que permite codificar un diagrama de flujo o un diagrama de estados. Para explicarlo de una forma simplificada imaginemos que tenemos que programar un dispositivo de manera que inicialmente (le llamaremos estado Start) la máquina debe tener encendida una bomba para llenar un depósito. Pero para vaciarlo (llamado estado 2) un sensor de nivel debe indicar que el depósito está lleno (función de transición). Cuando estamos en el estado 2, la bomba se para y se abre la válvula de vaciado. Para pasar del estado 2 al estado “Start” (nueva función de transición) nuevamente el sensor de nivel tiene que estar a cero.
Con el anterior ejemplo, para transitar de un estado a otro, algo debe suceder. Este algo puede ser una presión, temperatura, campo magnético, tensión, etc. Es decir, una o varias señales indicadoras que obliguen a dejar de realizar lo que hacía, para pasar a una nueva tarea.
Inicialmente podemos pensar que una máquina de estados no es necesaria, porque con un If, else if, o else…while…etc es suficiente. Sin embargo, con una máquina de estados podemos conocer dónde nos encontramos en cada momento, simplificar el código, optimizar, ser eficiente y más profesional, etc.
La máquina de estados necesita de unas entradas y salidas para cada estado, y un conjunto de transiciones entre estados. De un estado, podemos ir a otro estado o a varios estados. Para llegar por ejemplo, al estado 5, se puede llegar directamente o pasando por los estados 1, 2, 3 y 4. En cualquier caso debe cumplir con unas funciones de transición. Al cambio entre estados se le conocer por transición.
Como indica el nombre de “máquina de estados finitos”, el número de estados es finito (limitado) y cada estado ocurre en un momento determinado. En la actualidad, no hay ordenadores comerciales capaces de procesar un número de estados infinito. Por ello muchas veces, aunque no es exactamente lo mismo, el concepto de máquina de estados y máquina de estados finitos se intercambia. Un ejemplo de máquina de estados infinitos sería el de un ordenador cuántico, algo que por ahora no se comercializa.
Otro ejemplo de máquina de estados infinitos es la máquina de Turing que dispondría de una memoria infinita.
¿Por qué emplear máquinas de estado finitas?
El empleo de una máquina de estados finitas permite conocer todas las condiciones de contorno del problema de forma completa y mucho más sencilla. Esto asegurará cometer menos errores y un comportamiento menos indefinido.
A considerar:
- No necesitamos ninguna máquina de estados hasta que la empleamos por primera vez.
- Muchas veces empezamos a programar un proceso que vamos mejorando y ampliando a lo largo del tiempo. Lamentablemente, puede llegar el momento en que nos demos cuenta que este proceso de mejoras y ampliaciones no lleva al final deseado.
El proceso básico para implementar una máquina de estados
Lo que hace interesante una máquina de estados es que permite describir de una forma muy completa la secuencia de un proceso. Existen tres puntos fundamentales en el proceso:
- Primero tener claro cuál es el problema: subir la puerta del garaje, regar las plantas, crear una máquina expendedora. Es decir, situarse delante del problema y entender que es lo que se pretende y con qué sensores y actuadores pensamos resolver dicho problema. Entender cuáles son nuestros recursos y limitaciones. Cuál es el objetivo u objetivos.
- Una vez tenemos claro que factores intervienen en el problema, representamos un diagrama de estados (Mealy o Moore) o un flujograma (UML o SDL) que a continuación describiremos.
- En base al anterior punto empezamos la codificación mediante una librería de Arduino u otro método que sea de nuestro dominio. Esta librería debe adaptarse perfectamente al punto anterior. Por ejemplo, hay librerías con las que sólo es posible estar en un estado a la vez.
A nivel profesional, es importante que el cliente esté en el proceso de definición de los estados y que todas las partes las interioricen. Eso permitirá conocer el buen o mal funcionamiento de la máquina de estados y en qué o cuales estados se produce un error (si los hubiera). Imaginemos que la máquina de estados no pasa del estado 15. Eso pudiera deberse a un error por ejemplo en la sensorización, un mal montaje o incorrecta interpretación de los datos. La máquina de estados ayuda y mucho a tener un buen control de todo el proceso.
Tipos de autómatas
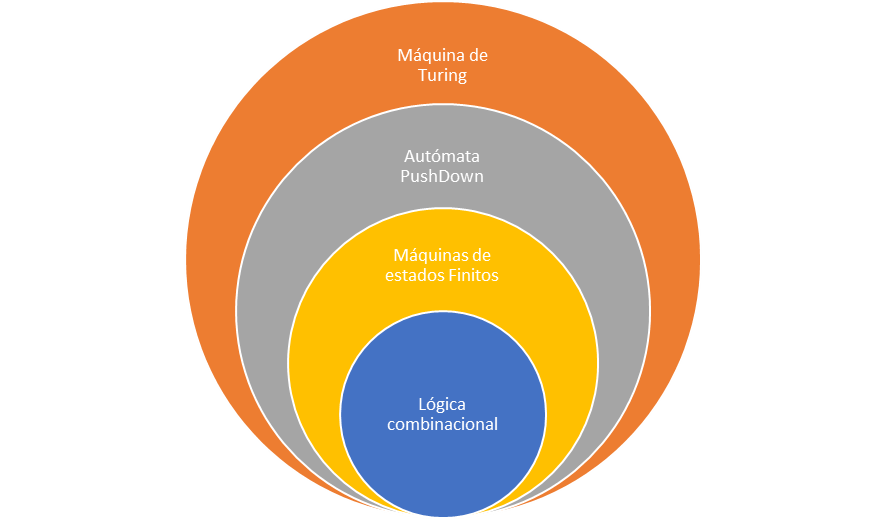
El mundo de los autómatas se divide en los siguientes conceptos:
- Lógica combinacional
- Máquinas de estados finitos
- Autómata Push-Down
- Máquina de Turing
La lógica combinacional
Todos los dispositivos en que las salidas dependen únicamente de las entradas en un momento dado sin tener en cuenta en ningún momento estados anteriores a las entradas o salidas, se basan en la lógica combinacional. La lógica combinacional también se la conoce por “sistema combinacional”.
La lógica combinacional carece de memoria y retroalimentación. Las funciones booleanas y el álgebra de Boole son algunos ejemplos. Por lo que la electrónica basada en funciones combinacionales, que emplean el álgebra de Boole, son los llamados circuitos combinacionales.
Máquinas de estados
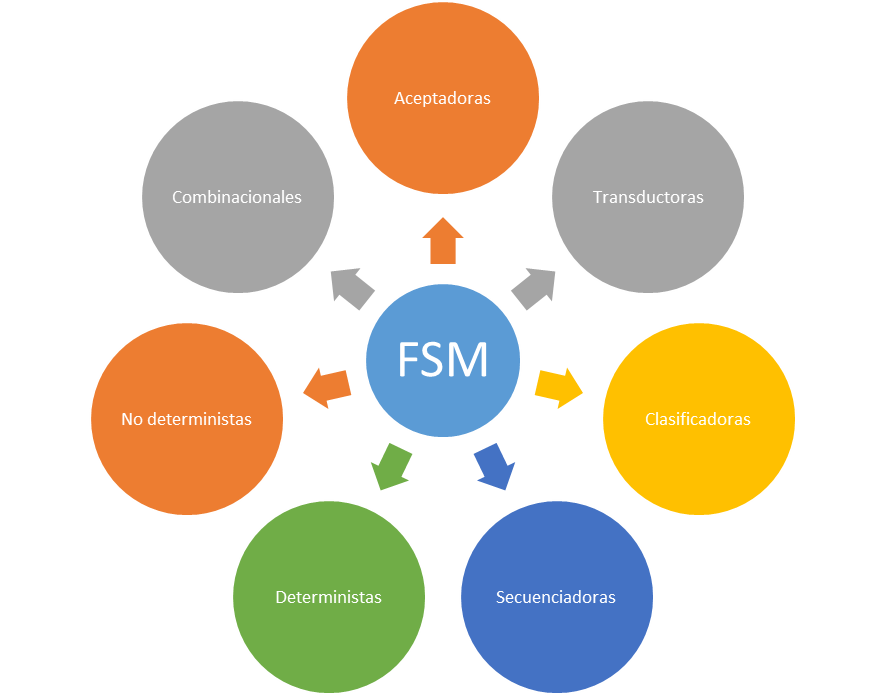
En general los tipos de máquinas de estados más conocidos son las siguiente:
- Las aceptadoras (reconocedoras o discriminadoras): Se llama aceptadora aquella que la salida es de forma binaria. Las máquinas aceptadoras se las conoce por autómatas finitos. La salida de cada estado de este tipo de máquinas, es una aceptación o no aceptación/rechazo. Los estados con salida positiva se les conoce como estados finales.
- Transductoras: Son un tipo de máquinas que son una variación de las aceptadoras. Son máquinas más generales y trabajan tanto de forma binaria como con otro tipo de datos. A este tipo de máquinas se le conoce como autómata. Las máquinas transductoras transforman un conjunto de señales de entrada en una secuencia de salida, pudiendo ser esta binaria o más compleja, dependiendo de la entrada actual (no sólo del estado) y pudiendo ser no necesario un estado inicial. Este tipo de máquinas son usadas para el control de dispositivos y en el campo de la computación.
- Clasificadoras: Las máquinas clasificadoras son una generalización de las aceptadoras con un array de salida n dónde n > 2.
- Secuenciadoras (reconocedoras, generadoras o detectoras): Éste tipo demáquinas realizan la detección de patrones o secuencias determinados en respuesta a las entradas recibidas. Transitan de un estado inicial a un estado final de “éxito”. Son útiles para la verificación de contraseñas, códigos, validación de paquetes de datos, etc.
- Deterministas (DFA): Cada estado tiene exactamente una transición para un input concreto. Las FSM deterministas siempre tienen una transición definida. Cuando la totalidad de las transiciones están determinadas en un Autómata, es decir para cada par de (estado, evento) existe uno y sólo un estado correspondiente, se tiene un Autómata Determinısta.
- No deterministas (NFA, GNFA): Una entrada para un estado concreto puede conducir a uno, más de uno o a ninguna transición. Si se tiene al menos una transición no definida o indeterminada entonces tenemos un Autómata No Determinısta.
- Combinacionales: Es aquella máquina de estados finita de un único estado que sólo transita dentro del mismo estado.
Las máquinas de estados nos rodean en la sociedad moderna: Por ejemplo, las máquinas expendedoras, las luces de tráfico, los ascensores, las puertas de acceso automáticas, tornos de acceso, un horno doméstico, la lavadora, etc. Posiblemente los inodoros de nuestros hogares se podrían simplificar como máquinas de estados.
Además, el uso de las máquinas de estado finitas es muy importante en distintas áreas, incluyendo la ingeniería eléctrica, la lingüística, las ciencias de la computación, la biología, la matemática, los videojuegos y la lógica.
La máquina de Moore
Este tipo de máquina de estados la salida depende sólo del estado. Las salidas sólo cambian si existe un cambio de estado. Las entradas serían los sensores (de temperatura, presión, campo magnético, etc), las salidas los actuadores (motores, servos, etc). La máquina de Moore al igual que la de Mealy, tiene entradas, salidas y transiciones. La lógica de salidas depende del estado dónde se encuentra el sistema. La ventaja del modelo de Moore es una simplificación del comportamiento. La máquina de Moore viene caracterizada por la siguiente expresión:
- Estado siguiente = f(estado actual, inputs)
- Salida = f(estado actual)
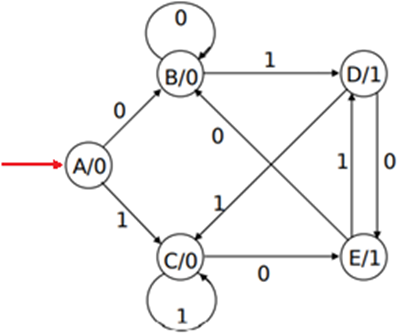
La máquina de Moore se representa de la siguiente manera:
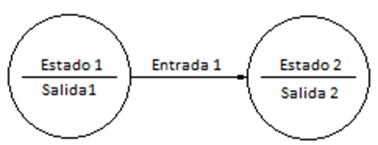
En el siguiente ejemplo de máquina de Moore, cada estado está representado por una letra. Las entradas y las salidas se representan por un 0 o un 1.
| ENTRADA | ESTADO ACTUAL | SIGUIENTE ESTADO | SALIDA |
| – | – | A | – |
| 0 | A | B | 0 |
| 1 | A | C | 0 |
| 0 | B | B | 0 |
| 1 | B | D | 0 |
| 0 | C | E | 0 |
| 1 | C | C | 0 |
| 0 | D | E | 1 |
| 1 | D | C | 1 |
| 0 | E | B | 1 |
| 1 | E | D | 1 |
En la primera fila, podemos observar que, si estamos en el estado A, con una entrada de 0, el siguiente estado será B y la salida 0.
La máquina de Mealy
La máquina de Mealy es una máquina de estados finita que emplea acciones de entrada, es decir, depende de la entrada y el estado. El uso de un FSM de Mealy conduce generalmente a una reducción del número de estados.
La máquina de estados de Moore y de Mealy hacen exactamente lo mismo, sólo que la de Mealy es más compleja de implementar.
- Estado siguiente = f(estado actual, inputs)
- Salida = f(estado actual, inputs)
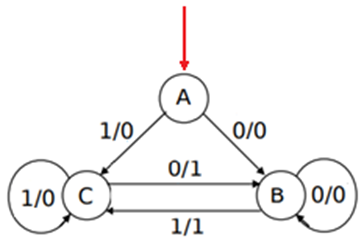
La máquina de Mealy se representa de la siguiente manera:
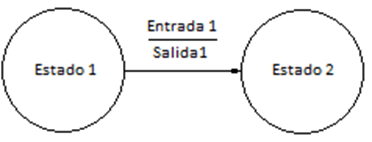
En el siguiente ejemplo, cada estado se representa por una letra, dentro de una “burbuja”. En la flecha se representa la entrada y la salida.
| ENTRADA | ESTADO ACTUAL | SIGUIENTE ESTADO | SALIDA |
| – | – | A | 0 |
| 0 | A | B | 0 |
| 1 | A | C | 0 |
| 0 | B | B | 0 |
| 1 | B | C | 1 |
| 0 | C | B | 1 |
| 1 | C | C | 0 |
En la primera fila indicamos que, si la entrada es 0 y estamos en A, pasaremos al estado B con una salida de 0.
La máquina de Turing
La máquina de Turing es un concepto creado por el matemático británico Alan Turing en 1936 en la revista “Proceedings of London Mathematical Society”. En sus orígenes era una máquina que manipulaba símbolos sobre una cinta de acuerdo a una serie de reglas.
La máquina de Turing presenta un modelo en el que se asientan todos los ordenadores actuales. Consta de los siguientes elementos: Una es una cinta larga infinita dividida en casillas dónde se escriben símbolos, por ejemplo, ceros y unos. Luego un cabezal que se mueve a través de esa cinta, y es capaz de leer y escribir estos símbolos. Finalmente, un programa que le indica al cabezal que es lo que tiene que hacer. Este programa puede estar escrito en la propia cinta. En los ordenadores actuales, la cinta es la memoria y el cabezal el microprocesador. En teoría, y no demostrado, cualquier programa se puede ejecutar en una máquina de Turing, y dichos programas pueden tardar más o menos en el tiempo en ejecutarse.
REPRESENTACIÓN DE LAS MÁQUINAS DE ESTADOS CON EL LENGUAJE UML Y SDL
La representación de las máquinas de estados se realiza de distintas maneras. En general hay dos lenguajes principales uno es mediante el lenguaje UML y el otro mediante el lenguaje SDL.
Ambos no son lenguajes de programación propiamente, sino que son instrumentos que ayudan a programar una máquina de estados, que es el tema que estamos desarrollando.
El UML y SDL, son lenguajes de especificación y de diseño basado en diagramas y gráficos. Por tanto, sus elementos son visuales de manera que se facilita la comprensión y el aprendizaje por parte de una persona.
El modelo de lenguaje unificado (UML)
El modelo de lenguaje unificado en inglés (UML) permite superar las limitaciones de las máquinas tradicionales de estados finitos al tiempo que conservan sus principales beneficios. Las máquinas de estado UML introducen nuevos conceptos de estados jerárquicamente anidados y regiones ortogonales, al tiempo que amplían la noción de acciones. Las máquinas de estado UML tienen las características de las máquinas de Meal y de Moore. Admiten acciones que dependen tanto del estado del sistema como del evento desencadenante, además de poseer características típicas de las máquinas de Meal dónde las acciones de entrada y salida están asociadas con estados en lugar de transiciones como en las máquinas de Moore.
El lenguaje UML no es como tal un lenguaje de programación, sino representa la realidad de un requerimiento.
- El UML es un estándar internacional desde el 2004 mediante la norma ISO/IEC 19501:2005 Information technology — Open Distributed Processing — Unified Modeling Language (UML). Con la versión 1.4.2. La norma se actualizó en el año 2021 a la versión 2.4.1 la cual corresponde a la ISO/IEC 19505-1.
- En el año 2012 se actualizó la norma a la última versión definitiva disponible, la 2.4.1, generando la norma ISO/IEC 19505-1.
Existen varios tipos de diagramas dentro del lenguaje UML, por lo que los diagramas de estados no son los únicos que existen en dicho lenguaje. En general el lenguaje UML se puede clasificar dentro de dos tipos, los diagramas estructurales y los diagramas de comportamiento.
Recomendación: puede representar una máquina de estados empleado el lenguaje UML con la herramienta plantUML: plantuml.com
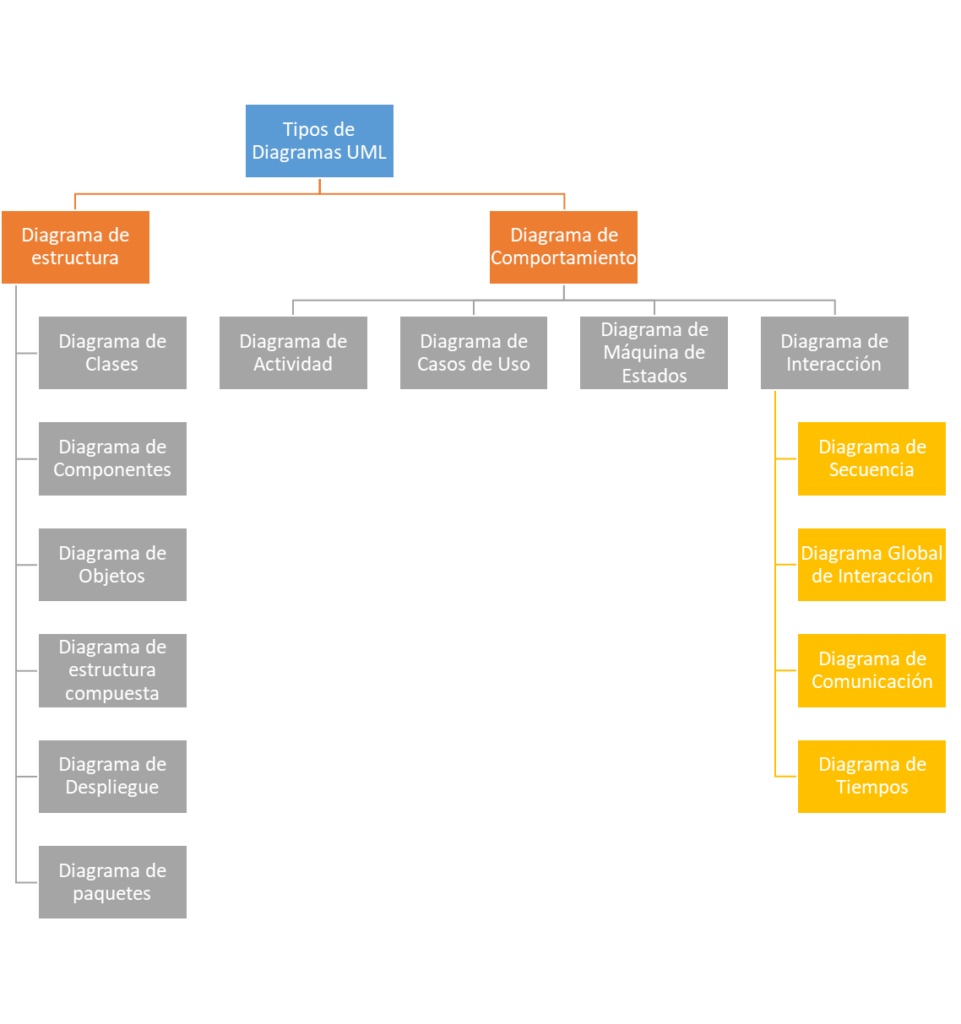
Dentro de los diagramas estructurales tenemos:
- Diagrama de clases.
- Diagrama de componentes.
- Diagrama de despliegue.
- Diagrama de objetos.
- Diagrama de paquetes.
- Diagrama de estructura compuestas.
A partir del UML 2.5 se añadió otro diagrama estructural, llamado “diagrama de perfiles”.
Dentro de los diagramas de comportamiento:
- Diagrama de actividades.
- Diagrama de casos de uso.
- Diagrama de máquinas de estado.
- Diagramas de integración.
- Diagrama de secuencia.
- Diagrama de comunicación.
- Diagrama de tiempos.
- Diagrama general de interacciones.
Representar un diagrama de estados con el UML
Cuando veamos un diagrama de estados veremos rombos, cajas, flechas y círculos dónde cada uno de estos símbolos tiene un significado especial que hay que conocer para poder hacer una correcta representación de lo que se quiere realizar.
Estado (do)
Los estados se representan con rectángulos de esquinas redondeadas que se etiquetan con el nombre del estado.

Los estados están interconectados mediante transiciones. Dentro de un estado se puede dar una descripción de lo que es el estado. Los estados pueden estar activos (el estado está llevando a cabo un trabajo) o inactivos (el estado no está trabajando). Si la máquina de estados tiene concurrencia varios estados pueden estar activos. Sino tiene concurrencia sólo un estado está activo.
Los Pseudoestados
Un pseudoestado no es como tal un estado, sino algo que sucede durante la transición. Pueden haber de varios tipos, de opción, de unión, de entrada y de salida.
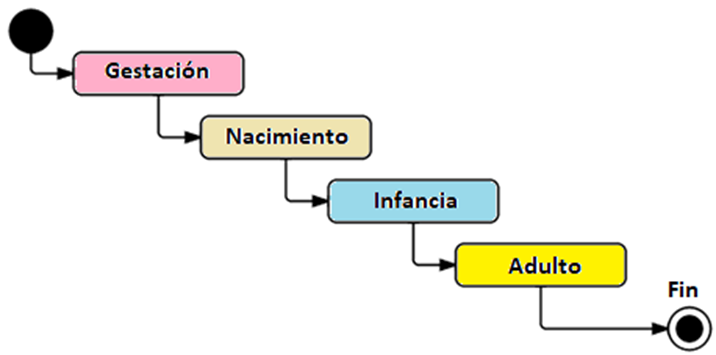
Pseudoestado Start o Inicial
La forma de indicar que en un punto determinado del diagrama se inicia el proceso es mediante un círculo pintado de negro seguido de una única flecha de transición. Es el punto de entrada a la máquina.

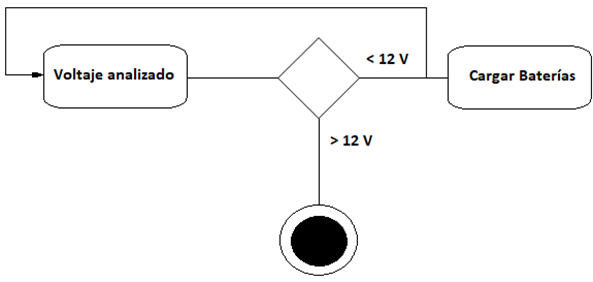
Pseudoestado de opción o decisión
Un símbolo con forma de rombo o diamante es el lugar se ramifican las distintas posibilidades. Puede tomar una ruta u otra según una determinada condición.

Da información sobre lo que sucede durante las transiciones. En el siguiente ejemplo mostramos un ejemplo de cómo actuaría un supuesto cargador de baterías. Si el voltaje supera los 12 V finaliza el proceso, pero si es inferior, se cargan las baterías.
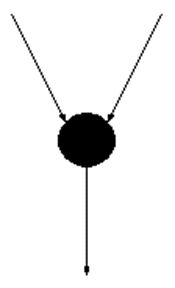
Pseudoestado de unión
Permite que varias transiciones converjan a una sola o que se bifurque a otras transiciones dependiendo de ciertas condiciones. Si esto sucede es más recomendable utilizar el anterior pseudoestado de opción.
De un estado pueden salir o llegar varias transiciones lo que generaría que de una “cajita” salieran varias flechas. Con el pseudoestado de unión el diagrama luce mucho más limpio y ordenado. El pseudoestado de unión se representa mediante un círculo relleno.
Pseudoestado de salida (Exit)
Cuando el proceso que sigue el diagrama o un estado compuesto finaliza (por error, por no estar completado o por un problema), la forma de representarlo es mediante un círculo con una cruz “X”.
Por ejemplo, imaginemos que un estado o estado compuesto tiene un error al ejecutar el código, la forma de salir es mediante este pseudoestado.

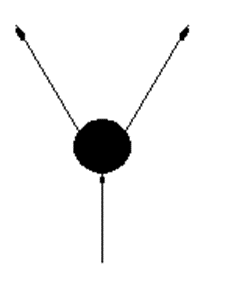
Pseudoestado fork
El pseudoestado fork, divide una transición o hilo de ejecución para que dos estados o más ocurran concurrentemente, es decir, a la vez. Se representa mediante una barra rellena.
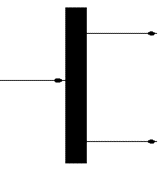
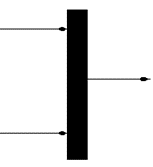
Pseudoestado de unión o Join
El pseudoestado de unión o join Une las concurrencias para tener un solo camino o hilo de ejecución. Todos los estados deben finalizar para que la unión tenga lugar por tanto no se podrá viajar a otro estado. Se representa mediante una barra rellena.
Estado compuesto
Un estado que contiene subestados anidados. En otras palabras, es un estado agrupador de estados. La caja en rojo, agrupa cuatro estados, esto es un estado compuesto.
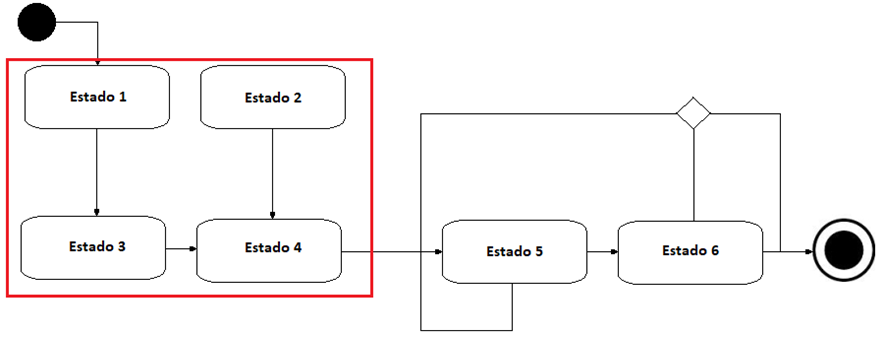
Es como si tuviéramos un estado dentro de una máquina de estados.
Estado Compuesto Ortogonal
Si es necesario que dos estados diferentes se ejecuten al mismo tiempo, porque son concurrentes, se emplearán los estados compuestos ortogonales.
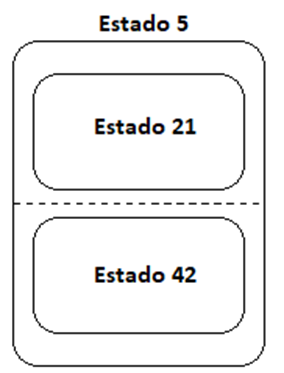
Subestado
Un subestado es un estado o conjunto de estados que se encuentra dentro de un estado compuesto.
Finalizador
La forma de representar que un proceso ha finalizado es mediante un círculo con un punto oscuro en el interior.

Transición
Una transición en el lenguaje UML es una flecha. Éstas muestran el sentido en que el diagrama fluye de un estado a otro. Las transiciones conectan un estado con otro. Las transiciones pueden llevar una etiqueta encima la flecha (también llamada firma). Dan más información de lo que sucede en la transición. Es recomendable usarlas.

Las etiquetas pueden tener tres partes, gatillo o evento, guarda, efecto.
Evento o Gatillo
Un evento o un gatillo es aquel suceso que hace que nos movamos de un estado a otro. Es decir, aquel acontecimiento que activa una transición. Se etiqueta encima de la flecha de la transición que tiene lugar. En el siguiente esquema el evento es: “suena el despertador” y la transición es la flecha.

Un ejemplo muy sencillo de estados sería el caso de una habitación iluminada por una bombilla. Hay dos estados, habitación iluminada y habitación a oscuras. Al pulsar un interruptor se enciende la bombilla. Por lo que la acción de pulsar el interruptor sería otro sencillo ejemplo de transición.
La guarda
La guarda es la condición que se debe cumplir para llevar a cabo la transición. Por ejemplo, pulsar el interruptor de noche a las 6 de la mañana para pasar al estado iluminar habitación.
Comportamiento transicional o efecto
Un comportamiento que resulta cuando un estado pasa por una transición. Se escribe arriba de la flecha de transición. Es la actividad que está sucediendo durante la transición (no después).
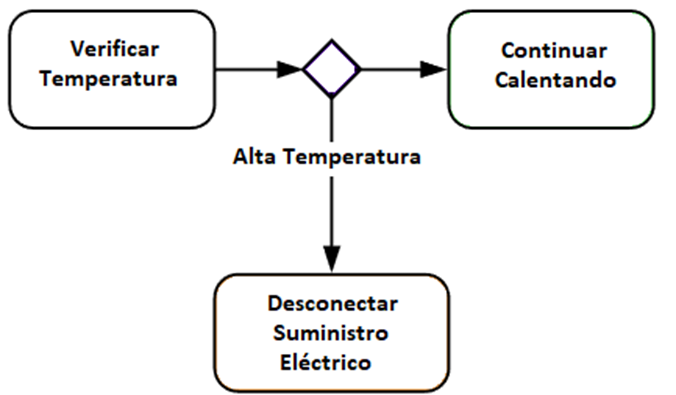
Disparador
El disparador se parece a un evento. Es un suceso que cuando tiene lugar se transita de un estado inicial a otro. Un disparador se sitúa después de un pseudoestado. El disparador se escribe encima de la flecha de transición.
Nos encontraremos un disparador cuando después de un estado tengamos que elegir entre varias opciones y según la opción se transiciona a un estado u otro.
Historial
El historial recuerda los estados pasados. Si el estado compuesto se interrumpe por cualquier razón, la historia permite volver a un estado. Los hay de dos tipos el Deep y el Shallow.
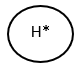
Historia Deep
- Tiene una memoria profunda.
- Regresa al estado más reciente donde se encontraba el estado.
- Se representa con un círculo y una “H*” en su interior.
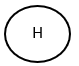
Historia Shallow
- Regresa al estado más exterior o al estado Start.
- Se representa con un círculo y una “H”.
A modo de ejemplo, imaginemos que estamos trabajando con un ordenador y hay un corte del suministro eléctrico. Si tenemos una Historia Deep, cuando reiniciemos el ordenador volverá al punto más cercano de dónde estábamos y se abrirán los programas, pantallas, etc. que previamente teníamos.
Sin embargo, si la historia es Shallow, se reiniciará todo el ordenador y perderemos la información última que teníamos.
EL LENGUAJE SDL
El lenguaje de especificación SDL es el acrónimo de Specification and Description Language. La descripción y especificación del lenguaje (SDL en inglés) es estándar de la UIT (Unión Internacional de Telecomunicaciones) e incluye símbolos gráficos para describir las acciones en una transición:
- Enviar un evento
- Recibir un evento
- Inicializar un temporizador o “timer”.
- Cancelar un temporizador o “timer”
- Inicializar otro estado concurrente
- Decisión.
El SDL incorpora tipos de datos básicos llamados «Tipos de datos abstractos», un lenguaje de acción y una semántica de ejecución para hacer que la máquina de estado finito sea ejecutable. El SDL es lo más próximo a la programación posterior real.
Arquitectura del lenguaje SDL
El lenguaje SDL está compuesto por bloques. Un conjunto de bloques es un sistema, un conjunto de procesos es un bloque y las instrucciones definen a cada proceso.
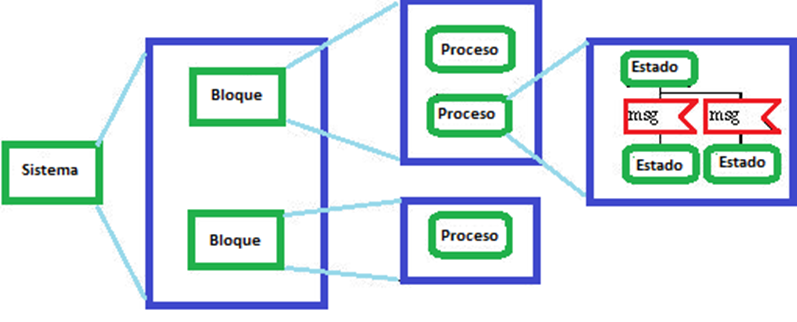
La entidad de mayor nivel es el sistema. Éste está rodeado por una frontera y se comunica con su entorno por medio de señales.
Los bloques agrupan los procesos que realizan funciones determinadas y se comunican entre ellos mediante canales.
Los procesos son máquinas de estado finitas. Las transiciones entre estados ocurren cuando se recibe una señal válida de otro proceso (o instancia), del entorno o del temporizador. Durante el proceso de transición se pueden realizar operaciones, llamar a un procedimiento o instanciar otros procesos. Las señales recibidas por un proceso son las conocidas por señales de entrada y las enviadas son las señales de salida.
Un canal es un medio para transportar señales entre uno o dos bloques y su entorno. Cada canal tendrá un listado de señales que transporta.
La información entre procesos que viaja por los canales, son las señales. Su declaración se realiza mediante un cuadro de texto el contenido de la cuál empieza por la etiqueta SIGNAL con el nombre de las señales seguido opcionalmente y entre paréntesis, del tipo de parámetro.

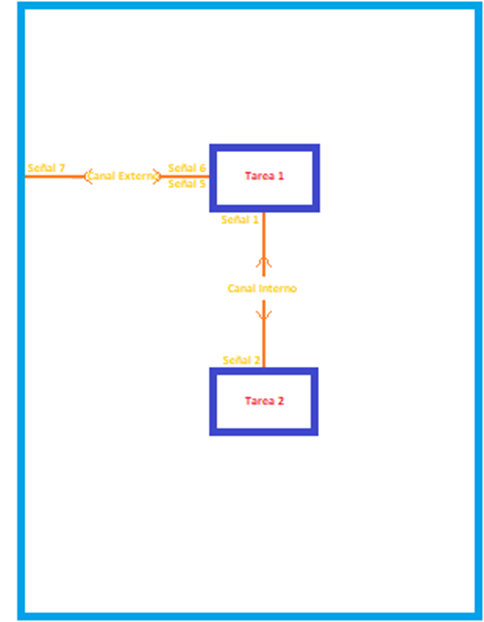
Comunicación
Cómo hemos indicado, los bloques están conectados a través de canales que intercambian mensajes o señales
Include
El include es un elemento que se emplea para añadir las librerías en el sistema. Según el lenguaje de programación se escribe de formas diferentes.

Texto
Contiene la declaración de estructuras, temporizadores, señales y variables. En este último caso se pueden declarar las palabras reservadas que según el lenguaje puede variar: Integuer, Char, String, Boolean, etc.
Inicio
El inicio se simboliza con la siguiente forma e indica el comienzo de un proceso.

Estado
Para simbolizar un estado lo hacemos mediante el siguiente símbolo:

Entradas
Las entradas se simbolizan mediante la siguiente forma, después de un estado. Es la expresión de una señal que permite una transición de estados.

Salidas
Es un elemento que representa el envío de una señal.

Tarea
Tarea empleada para la realización de tareas.

Decisión
De la misma manera que en el lenguaje UML este símbolo permite ir de un estado a otro de entre varias rutas.

Conector
Este elemento se emplea para realizar saltos condicionales.

Paro
Para señalar que un proceso ha finalizado lo hacemos con una cruz.

Procedimiento de llamada
Llama a un procedimiento que ha sido declarado previamente.

Procedimiento de referencia
Llamada a un procedimiento en un determinado proceso.

Inicialización de un procedimiento
El siguiente símbolo indica la inicialización de un procedimiento.

Devolución de un procedimiento
Devuelve el procedimiento el cual fue llamado.

Otros lenguajes
Existen otros lenguajes para representar las máquinas de estados. Por ejemplo, existen herramientas para modelar y diseñar la lógica de algunos controladores integrados. Éstos combinan máquinas de estado jerárquico (que generalmente tienen más de un estado actual), flujogrmas y tablas de verdad en un único lenguaje, lo que resulta en un formalismo y un conjunto de semántica diferentes. Estos gráficos, al igual que las máquinas de estado originales de Harel, admiten estados anidados jerárquicamente, regiones ortogonales, acciones de estado y acciones de transición.
Aplicaciones en Software
Los siguientes conceptos son los que normalmente se usan para hacer programas con máquinas de estado finitas:
- Programación de autómatas
- Máquina de estado finito basada en eventos
- Máquina virtual de estado finito
- Diseño de patrones de estado.
Máquinas y compiladores de estado finito
Los autómatas finitos se utilizan a menudo en el frontend de los compiladores de los lenguajes de programación. Éste frontend puede estar constituido por varias máquinas de estado finito que implementan un analizador léxico. A partir de una secuencia de Strings, el analizador léxico crea una secuencia de tokens de lenguaje (tales como palabras reservadas, literales e identificadores) a partir de los cuales se genera un árbol de sintaxis. El analizador léxico maneja las partes regulares y libres de contexto de la gramática de un lenguaje de programación.
MÁQUINAS DE ESTADO EN ARDUINO
El repositorio de Arduino posee una librería gratuita de D. José Rullán llamada “Statemachine” que implementa una máquina de estados simple. Se descarga directamente del repositorio de Arduino o también se puede descargar del GitHub. Esta librería es compatible con todas las arquitecturas por lo que es posible emplearla en todas las placas de Arduino.
La librería “Statemachine” se implementa en un sketch definiendo la lógica de estados en forma de funciones. Las transiciones se implementan también mediante funciones que devuelven un valor booleano y el número del estado posterior.
La lógica de estados y sus transiciones condicionales se implementan mediante funciones permitiendo una mayor flexibilidad. La máquina de estados que ofrece la librería es determinista, lo que significa que sólo se puede estar en un estado en un tiempo determinado y las transiciones sólo ocurren cuando la función de transición devuelve “true” (aceptadora). Si se definen múltiples transiciones para un estado determinado, sólo la primera en ser leída modifica el estado actual.
Estados
Hay dos maneras de declarar un estado lógico:
- A través de una función lambda (una función anónima) declarada mediante el método machine.addState().
- Definiendo la función y pasando la dirección al método addState().
Los estados contienen la lógica de la máquina del programa. La máquina sólo evalúa el estado actual hasta que tiene lugar en una transición lo que apunta a otro estado.
Para evaluar una parte del código mientras la máquina está en un estado en particular, se puede utilizar el atributo machine.evaluateOnce. Es cierto que cada vez que la máquina entra en un nuevo estado hasta que evalúa la primera transición.
Transiciones
Cada estado tiene las transiciones definidas en el Setup(). Las transiciones requieren dos parámetros.
- La función de la transición devuelve un valor booleano indicando si la transición ocurrió o no.
- El número del estado de destino. El estado de destino se puede especificar mediante el puntero de estado. Éste podría apuntar al mismo estado en el que se encuentra, si desea establecer dinámicamente el objetivo de la transición. Para hacerlo, se emplea state -> setTransition(). Debe pasar el índice de la transición que desea modificar y el número del estado de destino.
Las transiciones son evaluadas por la máquina de estados después que se haya ejecutado la lógica de estado. Si la transición no se evalúa como cierta (true), la máquina se mantiene en el mismo estado.
Ejemplo de Estados
El estado lógico se define en una función al cual se le suministra como un parámetro al método machine.addState() :
State* Start = machine.addState(&stateStart);
Aquí el estado “stateStart” es el nombre de la función que define la lógica del estado Start. La función se define en el sketch. Por ejemplo:
void stateStart(){
Serial.println("State Start");
if(machine.executeOnce){
Serial.println("Execute Once");
digitalWrite(LED,!digitalRead(LED));
}
}
State Execute Once
Si se requiere la ejecución de una porción de código dentro de un estado sólo una vez, se puede usar el atributo de la máquina executeOnce. Este atributo es “true” la primera vez que el estado lógico se evalúa y entonces se convierte en un falso hasta que la transición hacia el nuevo estado tiene lugar. En el ejemplo anterior, el LED se activa una vez por cada vez que la máquina entra en el estado Start.
Transiciones
Las transiciones se añaden al estado en la función setup(). Cuando se especifica una transición a un estado se le suministra el nombre de la función que evalúa la transición y el estado objeto al que la máquina debe ir cuando se devuelve un true.
S1->addTransition(&transitionS1S2,S2); // S1 transición a S2
Las transiciones se implementan evaluando una función que devuelve un valor booleano de true o false. Si la función devuelve un true, la máquina pasará del estado actual al nuevo estado que fue especificado dentro de la función setup().
bool transitionS1S2(){
if(digitalRead(5) == HIGH){
return true;
}
return false;
}
Cada estado puede tener múltiples transiciones, y cuando el estado está activo (estado actual de la máquina) se evalúan todas sus transiciones para determinar el siguiente estado activo. Cuando un estado dispone de varias transiciones, las transiciones se evalúan en el orden en que se agregaron al estado. La primera transición en devolver un true determinará el siguiente estado activo.
Transición a otro estado
Con esta librería se puede forzar una transición a otro estado llamando al método transitionTo(State* s). Este método acepta un puntero a un estado específico a un “int” que represente el índice del estado. La forma más sencilla es empleando un puntero. Por ejemplo:
machine.transitionTo(S8);
Cuando se evalúa esta línea de código, la máquina se moverá a la transición S8.
Modificando el objetivo de una transición
Es posible modificar dinámicamente el destino de una transición definida mediante el método setTransition(int index, int stateNo).
randomState = random(0,6);
Serial.print("Transitioning to random state ");
Serial.println(randomState);
S0->setTransition(0,randomState);
En este ejemplo, a la primera transición (0) agregada a S0 se le asigna un destino aleatorio mediante un random que va de 0 a 5. Suponiendo que la máquina tiene seis o incluso más estados, cada vez que se ejecuta este código se transita desde S0 a un estado diferente.
Otras librerías del repositorio de Arduino
En el repositorio de Arduino podemos encontrar las siguientes librerías:
- Arduino-FSM: Autor Jon Black. Sólo compatibles con la arquitectura AVR, es decir, Arduino micro, Leonardo, Mega, NANO, UNO y Yún.
- Finite State Machine: Autor: Arekushi. Compatible con la arquitectura AVR, es decir, Arduino micro, Leonardo, Mega, Arduino NANO, UNO y Yún. Proporciona un modelo de máquina de estados orientado a objetos aplicados en C++ para ser empleado en robots que sigan por ejemplo líneas.
Conclusión
La representación de un proceso mediante un diagrama de estados (máquinas de Mealy o Moore), lenguaje UML o SDL (u otros) y su posterior codificación permite representar e implementar una secuencia lógica de estados, reduciendo el número de errores y aumentado el rendimiento.
En este post se ha intentado resumir la idea principal de las máquinas de estado, los tipos principales, los diagramas de estado y lenguajes más empleados, para finalmente conocer y emplear algunas de las librerías más utilizadas en Arduino.
BIBLIOGRAFÍA
- [1]. Tutorial de diagrama de máquina de estados | Lucidchart
- [2]. Introducción a SDL. DAVID ESTEBAN SASTRE. pdf
- [3]. SINTAXIS Y SEMÁNTICA DE LOS LENGUAJES (UTN-FRR) DE LA CARRERA DE INGENIERÍA EN SISTEMAS DE INFORMACIÓN. AUTÓMATAS PUSH-DOWN Y MÁQUINAS DE TURIN. GUÍA TEÓRICO-PRACTICA PARA ALUMNOS DE LA CÁTEDRA. ING. EDUARDO AMAR. Pdf
- [4]. Wikipedia: Finite-state machine. Finite-state machine – Wikipedia
- [5]. Wikipedia: Autómata finito. https://es.wikipedia.org/wiki/Aut%C3%B3mata_finito
- [6]. Documentación y repositorio de Arduino. State Machine: https://www.arduino.cc/reference/em/libraries/statemachine/ Autor: José Rullán.
- [7]. Blog Arduino: https://www.joober.eu/blog-arduino/
